众所周知,选择示波器时经常会用到5倍法则,其实不仅仅是针对带宽,当涉及到快沿信号上升时间测试时,根据上升时间选择示波器也会用到5倍法则。本文将分别对这两种情况下的5倍法则展开讨论,并介绍当考虑示波器和探头构成的整个测试系统时又该如何选择。
1. 示波器带宽选择时的5倍法则
所谓5倍法则,就是为了保证信号的幅度测试精度,示波器的带宽至少要选择为信号频率的5倍!这通常针对于正弦波信号,因为其频谱只有一根谱线。而对于脉冲信号,由于理论上具有无数个谐波,通常将示波器带宽选择为所关注的最高次谐波频率的5倍。
为什么按照5倍法则选择示波器的带宽呢?如果不按照这个法则,对于信号幅度测试精度有多大影响呢?选择示波器带宽时,5倍法则主要适用于哪一类示波器?
为了解释这些问题,首先需要了解一下示波器的模拟带宽。示波器的模拟通道具有低通滤波器的频率响应,带宽就是指该低通滤波器的3dB截止频率。如果测试一个频率与示波器标定带宽相同的正弦波信号,电压幅度测试结果将下降为真实电压值的0.707倍,如果用对数表示,则测量幅度将降低3dB。
可将示波器的模拟通道等效为一个RC低通滤波器,为了简便起见,此处只考虑一阶RC低通滤波器,其等效电路及幅频响应如图1所示。一阶RC低通滤波器的幅频响应表达式可写为:
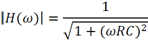
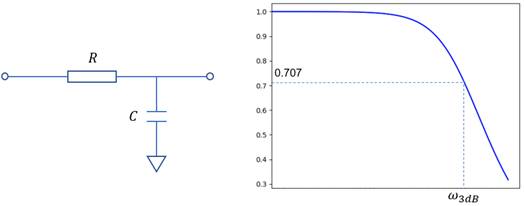
图1. 一阶RC低通滤波器电路模型及其幅频响应
使得传输系数下降至0.707时的频率称为低通滤波器的截止频率,或者称为3dB带宽,据此可得
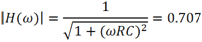
经计算得
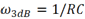
代入幅频响应函数后得
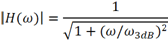
由图1中的幅频响应可知,随着频率的不断提高,信号经过滤波器时的衰减越大,这也意味着测得的信号幅度误差越大。如何保证信号的幅度测试精度呢?
很明显,当示波器的带宽远远大于信号的频率时,才可以得到非常高的幅度测试精度。但是,示波器带宽越大,成本越高,实际选择时必须折中考虑成本和测试精度。业界通常采用5倍法则选择示波器的带宽,此时可以保证至少98%的幅度测试精度。
假设待测正弦波信号的幅度为1V,角频率为ω0,当测试精度不低于98%时,则满足如下关系式

进一步化简可得
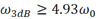
这表明,当测试正弦波信号时,只有在示波器的带宽不低于正弦波信号频率的4.93倍时,才能保证至少98%的测试精度。为了方便,通常建议示波器带宽至少为信号频率的5倍,这就是5倍法则的由来。
表1. 测试不同频率的正弦波时对应的幅度精度

至于是否按照5倍法则选择示波器的带宽对测试精度有多大影响,在示波器带宽固定的情况下,表1给出了不同频率的正弦波信号对应的理论测试精度。显然,示波器带宽相对于信号频率越大,幅度测试精度越高!
选择示波器时必须要遵循5倍法则吗?可以肯定的是,带宽大是有好处的,尤其是针对于经济型的示波器而言(BW≤1GHz)。因为通常并不会对这类示波器的频率响应做相应补偿,其幅频响应平坦度并不好。而且,这类示波器模拟通道基本就是1阶RC低通滤波器的频响,如果要求98%的测试精度,就要按照5倍法则选择示波器带宽。
而对于中高端示波器,示波器内部通常都引入了模拟通道的补偿算法,可以得到比较平坦的幅频响应,因此,对于这类示波器可以不按照5倍法则进行选择。值得一提的是,对模拟通道的补偿并不会扰乱测试,相反,可以大大改善测试效果,提高信号保真度,尤其是针对于宽带信号以及高速数字信号的测试,这种补偿是至关重要的。
2. 示波器结合探头使用时,测试系统的带宽如何确定?
前面介绍了选择带宽时5倍法则的由来,接下来介绍当示波器结合探头使用时,整个测试系统的带宽由谁决定,并为下一步推导上升时间的级联公式做准备。
与示波器的模拟通道类似,探头也呈现为低通滤波器的频率响应。很明显,当示波器带宽远远大于探头带宽时,系统的带宽取决于探头;当探头的带宽远远大于示波器的带宽时,系统的带宽取决于示波器。
通常认为,测试系统的带宽和示波器及探头的带宽满足如下关系:
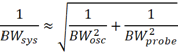
其实,当示波器带宽和探头带宽相当时,采用这个公式计算得到的系统带宽的误差是比较大的。示波器和探头构成的测试系统的幅频响应表达式为
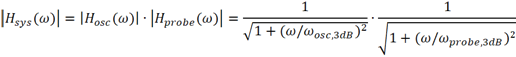
类似地,当系统的传输系数下降至0.707时的频率即为系统的3dB带宽,这意味着
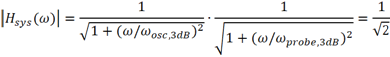
化简可得
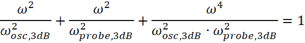
如果将上式中的高次项忽略,则便可以得到上面的结论。
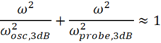
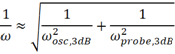
那么能否将高次项忽略呢?当示波器带宽和探头带宽差异较大时,高次项相对较小,是可以忽略的。二者带宽越接近,则忽略高次项带来的误差越大,当二者带宽相同时,使用上式计算的系统带宽的误差最大,可以达到25%的误差。但可以肯定的是,总体的系统带宽是小于示波器和探头带宽的!
尽管如此,对于中高端示波器和有源探头而言,由于可以对探头和模拟通道的频响做补偿,因此即使二者带宽相同,也可以满带宽使用。比如,示波器带宽为16GHz,探头带宽也为16GHz,则系统带宽也可以达到16GHz。而经济型示波器却没有这种补偿频响的功能,系统带宽会变窄,使用时要特别注意。
3. 按照上升时间选择示波器时的5倍法则
本节将首先介绍带宽与上升时间的关系,并给出理论推导;然后着眼于示波器和探头构成的整个测试系统,描述了系统的上升时间与示波器和探头的上升时间有着怎样的关系;最后道出结论,为了提高测试精度,建议采用5倍法则进行选择。
对于任意一个LTI (线性时不变)系统,当施加一单位阶跃信号时对应的零状态响应称为单位阶跃响应(简称为阶跃响应),该过程可以理解为其瞬态响应过程,响应的快慢取决于系统带宽,一般使用上升时间衡量。系统带宽越大,则瞬态响应速度越快,上升时间也越短。对于示波器和探头,亦是如此。
示波器和探头的上升时间与带宽之间具有怎样的量化关系?
示波器的模拟通道和探头均呈现为低通滤波器的特性,为了便于推导,此处假设二者均具有一阶RC低通滤波器的频响。
如果要确定上升时间,则需要从阶跃响应入手,一阶RC低通滤波器的阶跃响应为
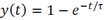
式中,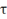 为滤波器的时间常数,且
为滤波器的时间常数,且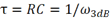 .
.
如果按照10%~90%的规则定义上升时间,则可以按照如下方法进行计算。
在t=0时刻,信号电压为0.
假设t1时刻,信号电压上升至0.1 V,则满足: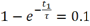 。
。
假设t2时刻,信号电压上升至0.9 V,则满足: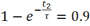 。
。
经计算可得上升时间为:

进一步化简得
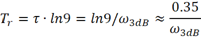
对于低通滤波器而言,3dB截止频率即为3dB带宽,因此可以得到关于带宽与上升时间关系的经典公式:
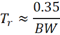
该公式是基于一阶RC低通滤波器频响推导的,对于BW ≤ 1GHz的示波器和探头而言,基本都适用。如果是更高带宽的中高端示波器和探头,其通道依然相当于低通滤波器,但通常并不是一阶低通滤波器的频响,所以上述公式中的系数不再是0.35,而是位于0.4~0.45之间。
对于示波器和探头构成的测试系统,总体的上升时间如何推算呢?
前面已经介绍了测试系统带宽与示波器和探头带宽之间的关系,结合带宽与上升时间的关系,则整个测试系统与示波器和探头的上升时间满足:

也就是说,整个测试系统的上升时间恶化了。
对于待测的快沿信号而言,定义其等效3dB带宽为BWsignal,与上升时间也可以近似等效于上面的关系式。如果使用示波器和探头测试该快沿信号,则信号等效3dB带宽的测量值与测试系统的带宽近似满足如下关系:
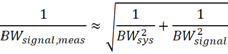
再根据带宽与上升时间的关系,将上式进一步化简得

由此可见,实际测量的快沿信号的上升时间与系统的上升时间有很大关系。
通常推荐测试系统的上升时间不大于待测信号上升时间的1/5,以提高测试精度,这就是在快沿测试过程中的5倍法则!
表2. 不同的系统上升时间对应的测试误差

表2给出了测试某一快沿信号时,不同的系统上升时间对应的测试误差。系统上升时间相对于信号上升时间越小,则测试误差越小,测试精度越高。当系统上升时间为信号上升时间的1/5时,测试精度可以达到98%。这也是在该测试场景下使用5倍法则的原因!
为了进一步验证,分别将示波器的带宽限定为1GHz、500MHz和200MHz,测试同一快沿脉冲信号的波形如图2所示。当带宽不足时,测试系统上升时间增大,严重恶化了测试精度。
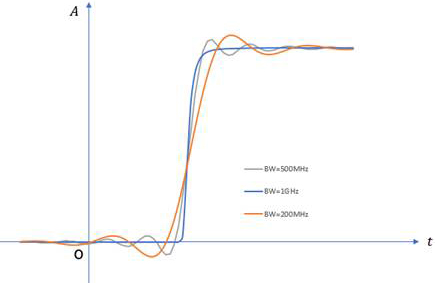
图2. 带宽分别限定为1GHz、500MHz和200MHz时测试同一快沿信号的结果
小结
本文描述并解释了在选择示波器时常用的5倍法则,该法则不仅适用于示波器带宽的选择,也适用于测试快沿信号时系统自身上升时间的选择。对于级联系统的等效带宽和上升时间,文中亦有描述。为了提高幅度和上升时间测试精度,强烈推荐采用5倍法则选择示波器。
作者:射频问问 Knight
